A. Istilah-istilah
- variabel bebas : yaitu variabel yang mempengaruhi atau disebut juga variabel independent
- variabel terikat : yaitu variabel yang dipengarui atau disebut juga variabel dependent
contoh judul penelitian :
- pengaruh pemberian asi pada bayi terhadap kecerdasan anak. (dari judul ini, maka variabel bebas nya: pemberian asi, dan variabel terikatnya: kecerdasan anak)
- pengaruh gaya kepemimpinan dan tata ruang kantor terhadap efisiensi kerja di PT Rahmadi Putra (variabel bebasnya ada dua yaitu gaya kepemimpinan, dan tata ruang kantor, sedangkan variabel terikatnya: efisiensi kerja)
Jumlah variabel bebas (independen) umumnya tidak dibatasi harus satu, dua atau tiga. Tetapi hal tersebut disesuaikan dengan kemampuan peneliti. Semakin banyak variabel bebasnya, maka akan semakin rumit, baik proses penelitiannya maupun olah datanya. Untuk variabel terikat biasanya hanya satu. Sehingga persamaan regresi yang umum adalah sebagai berikut :
Y=a+bX
Y= variabel terikat
a= konstanta
b= koefisien regresi
X= variabel bebas
B. Data penelitian
Data penelitian secara umum dikelompokkan menjadi 4 tingkatan:
1. data nominal : data kategori, yaitu data angka yang hanya merupakan simbol saja. Misal data jenis kelamin, pria=1, wanita=2. angka 1 dan 2 bukan angka sebenarnya. Jadi tidak dapat disimpulkan bahwa wanita lebih baik dari pria atau sebaliknya. Contoh lain data agama, islam=1, nasrani=2, yahudi=3. bukan berarti agama yahudi yang terbaik. Ciri data nominal, data ini tidak bisa digunakan untuk perhitungan matematis. Jadi misal islam+nasrani=1+2=3 jadi yahudi, bukan seperti ini. Ini tidak berlaku pada data nominal.
2. data ordinal : data kategori, tetapi antara data satu dan yang lainnya memiliki perbedaan, misal peringkat kelas, peringkat 1 tentu lebih baik dari peringkat 2 dan peringkat 3 dan seterusnya. Data jenis ini juga tidak bisa digunakan untuk perhitungan matematis. Angka 1, 2, 3, dst adalah simbol, tetapi diketahui bahwa angka peringkat 1 tentu lebih baik. Faham? He he he Atau contoh lain data tentang kepuasan menggunakan produk (sangat puas, puas, tidak puas).
3. data interval : data berjarak, antar kategori dapat diketahui selisihnya. Data ini juga tidak dapat dibandingkan atau dijumlahkan. Duh, gimana ya njelasinnya... emmm contoh aja ya: misal data suhu air atau suhu apa lah (misal air A=100 derajat, air B=200 derajat, air C=0 derajat. Bukan berarti air B 2 kali lebih panas dari air A, bukan berarti air C tidak memiliki suhu). Contoh lain tentang hasil belajar (A nilainya 40, B= 70, C= 80, D=0. bukan berarti kepandaian A hanya setengahnya C. Juga bukan berarti D tidak punya pengetahuan sama sekali)
4. data rasio : data angka numerik, bisa dilakukan operasi matematika, merupakan data hasil pengukuran, dapat diketahui selisihnya, dapat dibandingkan. Misalnya lama pendidikan SD 6 tahun, SMP 3 tahun, SMA 3 tahun, Sarjana 4 tahun. Jadi lama nya sekolah SD adalah dua kali lamanya sekolah SMP. Contoh lain tentang tinggi siswa, tentang jumlah gaji, dan lain-lain.
Udahhhh.... itu aja pengantar pendukungnya, kenapa saya menjelaskan masalah diatas, karena penting untuk pengetahuan sebelum melakukan analisis regresi. Karena analisis regresi membutuhkan data dengan syarat-syarat tertentu, antara lain datanya harus normal, supaya data normal dapat diakali dengan memperbanyak jumlah sampel. Data bersifat interval atau rasio dan sebagainya.
Langsung saja misalnya kita melakukan penelitian tentang pengaruh tinggi badan terhadap jarak lompatan pada olah raga lompan jauh misalnya. Dari judul ini, kita ingin menguji apakan tinggi badan seseorang itu mempengaruhi jarak lompatan atau tidak. Misalnya kita punya data seperti berikut ini:
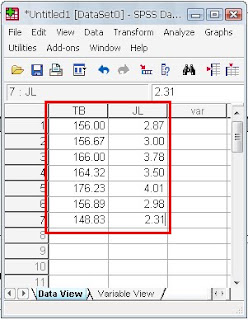
Data tersebut dapat diketik terlebih dahulu pada MS EXCEL, atau langsung pada spss, kalau saya lebih suka pake excel duluan. Alasannya untuk kepentingan edit, menghitung rerata, prediksi hubungan, juga manipulasi lebih mudah di excel.
Setelah data selesai, (asumsi saya, anda mengetik dulu di excel). Buka spss anda, tampilan pertamanya seperti ini:
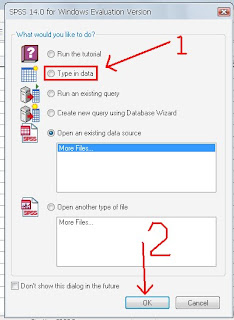
Pilih “type in data” kemudian klik OK. Sehingga muncul halaman seperti ini:
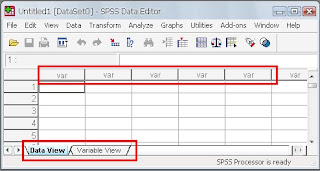
Disana yang saya beri tanda kotak, yang atas adalah var var var var... itu adalah nama variabelnya, nanti akan kita ubah sesuai kebutuhan. Terus yang saya kotak dibawah, ada dua tab, yaitu data view dan variabel view. Gambar diatas adalah tampilan data view, data view digunakan untuk memasukkan data nya, sedangkan tampilan variabel view seperti ini:
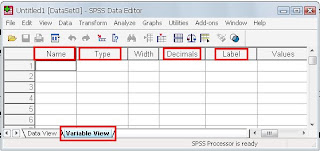
Yang perlu disesuaikan menurt saya hanya bagian “name” isikan nama variabel nya, disingkat saja lebih mudah, tetapi tidak boleh didahului dengan angka, misal 1a, 1b, 1c seperti itu tidak boleh. Harus huruf dulu, misal ada angka ya boleh, tapi tidak didepan, misalnya A1, A2, A3 seperti ini boleh. Contoh penelitian kita tadi kan variabelnya tinggi badan dan jarak lompatan, misan tinggi badan saya tulis TB, jarak lompatan saya tulis JL. Pada bagian “type” karena tinggi dan jarak adalah angka2 nanti datanya, maka saya pilih “numerik”. Kolom “decimal” digunakan untuk mengatur berapa angka dibelakang koma. Selanjutnya pada “label” anda boleh tulis lengkap nama variabelnya, misal “tinggi badan” dan “jarak lompatan” seperti ini tampilannya:
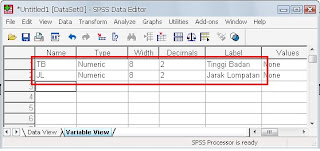
Setelah itu klik tab “data view” dan masukkan datanya seperti ini:

Tidak usah banyak-banyak, sekedar contoh kita punya 7 orang yang diamati misalnya seperti itu datanya. Kemudian langkah analisis regresi nya:
- klik menu “analyze” “regresion” klik “linear...”
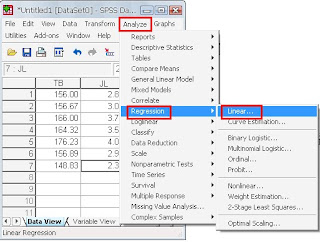
- sehingga muncul tampilan ini”
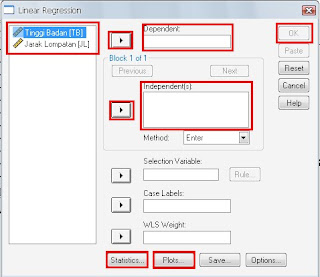
- perhatikan pada bagian yang saya kotaki saja, disana ada dua variabel yang tadi kita susun yaitu “tinggi badan [TB] dan jarak lompatan [JL]” klik tinggi badan, kemudian masukkan ke kolom dependent, caranya klik panah disamping kolom tersebut. Sehingga tampilan seperti berikut ini:
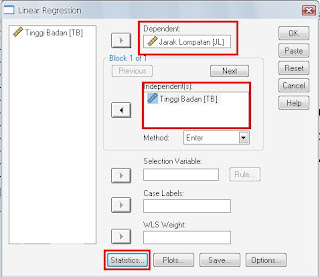
- Kemudian klik “Statistik” untuk menampilkan ukuran statistik yang dibutuhkan. Beri tanda centang yang dipilih
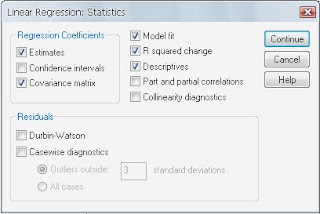
- Kemudian klik “continue” untuk kembali ke jendela sebelumnya. Setelah itu klik “plot” digunakan untuk menentukan grafik histogram dan normal plot.
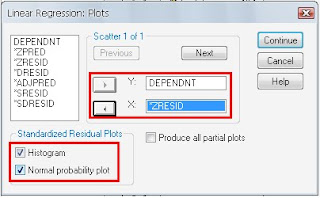
- Masukkan DEPENDNT ke X, dan ZRESID ke Y, kemudian beri tanda centang pada histogram dan normal probability plot. Klik “continue”.
- Selanjutnya klik “OK” dan tunggu spss sedang memproses data anda.
- Jreng..jreng....jreenggg..... muncul deh output nya seperti ini, akan saya jelaskan bagaimana membaca tabel-tabel nya.
- Output paling awal/atas ada judul, kemudian tabel ini:
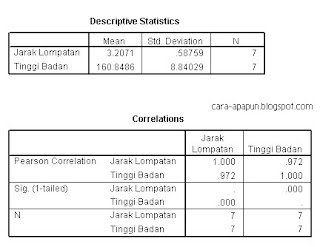
- Tabel descriptive statistic: menjelaskan bahwa yang dianalisis ada dua variabel, yaitu tinggi badan dan jarak lompatan. Juga disebutkan mean dan standar deviasi nya, N=7 berarti jumlah data yang kita olah ada 7 data/kasus.
- Tabel corelation: menunjukkan tingkat hubungan, tampilan ini sama persis ketika kita melakukan uji korelasi, tetapi pada uji korelasi biasanya ada keterangannya. Nah pembacaan tabel ini adalah disana terdapat “pearson correlation” berarti menggunakan korelasi pearson, kenapa otomatis begitu? Karena spss tahu jenis data nya rasio. Korelasi tinggi badan vs jarak lompatan = 0,972. (catatan: besarnya nilai korelasi antara -1 s/d +1). Sehingga angka 0,972 termasuk korelasi yang tinggi/signifikan. Pada “sig(1-tailed)” sebesar =0.000 ini dibandingkan dengan taraf signifikansi 5% = 0,05. jika sig(1-tailed) lebih kecil dari 0,05 maka terdapat korelasi yang signifikan. Sebaliknya jika angka sig(1-tailed) lebih besar dari 0,05 maka korelasi tidak signifikan. Hasil analisis diatas berarti ada korelasi yang signifikan.
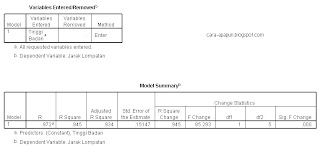
- Tabel variable entered/removed. Menjelaskan apakah ada variabel yang di hapus atau dimasukkan ke analisis. Disana variable removed tidak ada, berarti tidak ada data yang dihapus, berarti semua variabel dianalisis begitu maksudnya.
- Tabel model summary: menjelaskan besarnya presentase pengaruh variabel bebas terhadap variabel terikat. Lihat pada R square=0,945 yang berarti variabel tinggi badan mempengaruhi sebesar 94,5% terhadap variabel jarak lompatan, sedangkan 5,5% (100%-94,5%) dipengaruhi oleh faktor lain.
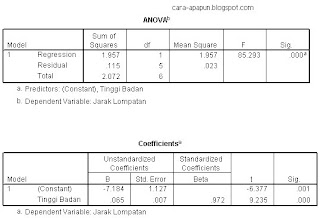
- Pada tabel anova, dapat diketahui apakah var bebas dapat menjelaskan variasi var terikatnya. Berdasarkan angka F =85,293 dibandingkan dengan F tabel pada df pembilang=1, df penyebut=6 diperoleh angka 5,99 untuk 5%, dan 13,74 untuk 1%. Cara pengambilan keputusan, jika F hitung > F tabel, maka var bebas dapat menjelaskan variasi var terikat.
- Tabel coefisien: digunakan untuk membuat persamaan regresi. Dengan mengambil angka pada kolom B, pada constant= -7.184 dan tinggi badan=0,065 berarti persamaan regresi nya:
Y = -7,184 + 0,065 X
- Output berikutnya hanya grafik saja, merupakan gambaran penyebaran data dalam bentuk grafik, tidak perlu saya lampirkan disini gambarnya.
Begitulah kira-kira cara melakukan analisis regresi berikut cara penginterpretasian output spss. Pada tutorial ini saya menggunakan spss 14, tetapi untuk versi yang lain, outputnya akan sama.
Semoga bermanfaat, kalau ada pertanyaan lain atau tentang statistik dengan spss, silahkan request pada bagian komentar, sebisa mungkin akan saya posting tutorial untuk anda.
Mau olah data online? Boleh saja dengan tarif yang sangat murah tentunya promosi!















0 comments:
Post a Comment
Sebelum meninggalkan halaman ini, silahkan kasih masukan pada blog ini...